Logique Tétravalente
Sommaire
Introduction: logiques multi-valuées
Par Norman Molhant
Les valeurs de vérité de la logique binaire usuelle sont vrai (T) et faux (F).
Depuis Aristote, à qui on doit l'exclusion d'un troisième terme (ce qui interdit qu'une assertion puisse avoir une valeur logique autre que vrai ou faux) et le principe de non-contradiction (qui interdit qu'une assertion puisse être à la fois vraie et fausse), la pensée moderne ne se permet que peu d'escapades en dehors du carcan dichotomique imposé par l'usage exclusif du raisonnement binaire en vrai/faux, bien/mal, pour/contre, 1/0, etc...
Et pourtant, on peut avoir diverses raisons pour vouloir utiliser plus de deux "valeurs de vérité".
1. Pour combler les «gaps» (manques) des valeurs de vérité
- Les assertions basées sur des présuppositions fausses.
Selon Strawson, des énoncés comme "L'actuel roi de France est chauve" ne sont ni vrais ni faux, ils ont plutôt une présupposition qui est fausse. On pourrait vouloir traiter ces cas en utilisant une troisième valeur de vérité (N) signifiant "ni vrai ni faux".
- Les futurs contingents.
Aristote lui-même souleva la possibilité que les assertions au sujet du futur ne soient ni vraies ni fausses au moment présent.
2. Pour clarifier les «gluts» (encombrements) des valeurs de vérité
On pourrait vouloir tenir compte de la possibilité que certaines assertions soient à la fois vraies et fausses. Cette idée peut sembler bizarre de prime abord, mais elle a été suggérée en réponse à certains paradoxes. Considérons l'assertion "Cette assertion est fausse" (une version compacte du paradoxe du menteur). Supposons qu'elle soit vraie. Alors, comme elle dit qu'elle est fausse, elle doit être fausse. Nous semblons donc avoir une preuve qu'elle est fausse. Mais si elle est fausse, alors ce qu'elle dit (c-à-d: qu'elle est fausse) est vrai! Nous avons donc aussi une preuve qu'elle est vraie. Une réponse aux paradoxes de ce genre est d'ajouter une nouvelle valeur de vérité (B) signifiant "à la fois vrai et faux".
(Note: la terminologie «gaps/gluts» est empruntée à Graham Priest: An Introduction to Non-Classical Logic.)
3. Pour des raisons épistémologiques
Certaines personnes veulent parfois ajouter une valeur de vérité pour "inconnu", de façon à permettre les trois valeurs de vérité "connu comme vrai", "connu comme faux" et "inconnu". Cela me semble toutefois une bien faible raison pour abandonner la logique classique. Il me semble plus approprié de garder la logique standard à deux valeurs et de traiter comme telle notre absence d'information au sujet de l'état de vérité de certains énoncés: notre ignorance de quelle colonne de la table de vérité correspond aux faits peut être elle-même une assertion traitable en logique binaire.
4. Pour distinguer entre différents types de vérité
On a suggéré, par exemple, de distinguer entre 5 valeurs de vérité: nécessairement vrai, vrai contingent, inconnu, faux contingent, nécessairement faux. De nouveau, cela me semble une mauvaise idée. Au lieu d'inventer une nouvelle valeur de vérité pour "nécessairement vrai", nous pouvons tenir compte de la nécessité ou de la contingence de la vérité d'un énoncé à l'aide d'un autre énoncé lui-même binaire.
Alors?
En fait ce ne sont aucune des raisons ci-haut qui motivent cette proposition de logique à quatre valeurs; le motif est plus simplement une insatisfaction profonde avec l'archaïque vision dichotomique du monde qu'impose la logique aristotélicienne.
Cette vision simpliste à l'extrême ne laisse la place à aucune des nuances exigées par le simple bon sens, par exemple pour décrire un conflit entre deux clans: les dirigeants d'un clan vont décrire le clan adverse comme l'axe du mal et leur propre clan comme l'axe du bien, opposition dichotomique qui leur offre l'exclusion du terme tiers pour proclamer faussement "qui n'est pas avec nous est contre nous" au mépris de ceux qui ne veulent, avec raison, prendre parti ni pour l'un ni pour l'autre clan, opposition dichotomique qui leur offre aussi le principe de non-contradiction comme paravent pour cacher hypocritement l'intérêt commun des dirigeants des deux clans à poursuivre ce conflit qui les maintient au pouvoir, opposition dichotomique qui permet enfin aux dirigeants des deux clans d'adopter une attitude identique, mutatis mutandis, sans éveiller le scepticisme des membres de leurs clans respectifs quant à la réalité et la logique de leurs proclamations respectives, pourtant diamétralement opposées.
Bref, la logique "aristo" (aristotélicienne) est devenue, par son simplisme extrême, une arme de désinformation, un instrument de maquillage, un outil de mensonge. Ainsi galvaudée, elle a perdu toute fiabilité et n'a donc plus guère de place dans l'outillage logique du chercheur et du penseur.
Comment?
En logique aristo, un sentiment ou un concept abstrait est tenu pour vrai ou pour faux sur simple proclamation complètement arbitraire, sans aucune justification logique. Il semble plus raisonnable de tenir pour ni-vrai-ni-faux tout ce qui est similairement invérifiable hors du champ d'une conscience individuelle ou collective.
De plus la logique aristo n'arrive pas à gérer de façon naturelle les indéterminations inhérentes à la physique moderne: superposition d'états quantiques, expérience du chat de Schroedinger, nature de l'électron et du photon, etc.. Il semble plus raisonnable de tenir pour à la fois vrai-et-faux toute réalité phénoménologique similairement potentielle ou partiellement indéterminée.
Bref, pour qu'une logique soit adaptée à l'état actuel de nos connaissances, elle doit permettre de manipuler non seulement le vrai et le faux, mais aussi le ni-vrai-ni-faux ainsi que le vrai-et-faux.
Pour éviter d'avoir à utiliser des formules potentiellement sources de confusion telles que « vrai (T) et faux (F) égale vrai-et-faux (B) », adoptons un système logique basé sur les valeurs élémentaires suivantes:
T : (strictly True) strictement-vrai, c-à-d: vrai-et-non-faux
(toute réalité vérifiable, mesurable, expérimentable);
F : (strictly False) strictement-faux, c-à-d: faux-et-non-vrai
(tout ce qui est irréel, situé hors de tout cadre de vérification);
B : (Both true and false) vrai-et-faux
(toute réalité phénoménologique potentielle ou partiellement indéterminée);
N : (Neither true nor false) ni-vrai-ni-faux
(toute réalité invérifiable hors du champ d'une conscience individuelle ou collective).
Copyright © 2005, 2006, Norman Molhant. Droit de copie et de diffusion accordés gratuitement à deux conditions:
- ne pas altérer ni retirer la mention du copyright avec ces conditions
- offrir gratuitement la consultation et le téléchargement de cette page
Pour en savoir plus : http://www.cafe.edu/sf/pl4c/
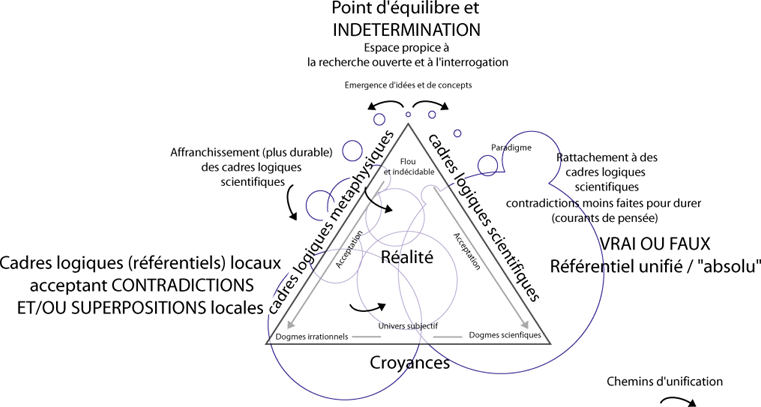
Logique Tétravalente, Metaphysique et Croyances
La logique tétravalente dans le contexte de l'affaire SBF
Synthèse : aspects epistémologiques
Concernant la logique tetravalente, il est à préciser que mon avis sur la question est extrêmement complexe et qu’il ne peut se réduire à mes brèves explications qui sont plus de nature à poser le contexte d’une problématique. Il est évident que la logique tetravalente peut être plus qu’une logique mathématique dans le sens des lettres ummites.
La question qu’il faut se poser dans les cas d’une construction ummite de la philosophie à partir d’une axiomatique tetravalente et ses équivalences fonctionnelles avec certaines philosophies sur Terre est cette recherche sur le fondement épistémologique de cette axiomatique.
- Sur quoi repose le formalisme ?
- Comment sont agencés les axiomes et les concepts ?
- Comment sont-ils construits ?
- Y a-t-il une logique plus fondamentale encore qui se réplique sur elle-même ses propres axiomes ?
- Voir aussi sur ce site : Epistémologie des logiques et logique tétravalente
Références
- pl4c par Norman Molhant
- Tétralogique par Denis Bolland
- Essai de Logique Tétravalente par Alban Nanty
| Cet article est une ébauche. Vous pouvez contribuer à ce travail en l'enrichissant. |