Comètes et Planète X

Cet article pose la question de la présence d'un corps gravitationnel massif à 120° d'inclinaison sur le plan de l'ecliptique par la présence d'un excès de densité cométaire dans le nuage d'Oort.

Un corps massif orbiterait-il loin des regards dans le nuage de Oort ? Le soleil aurait-il un compagnon sombre qui étendrait son influence sur les confins du système solaire ??

Questions souvent lues, entendues et qui prennent une résonnance plus particulière compte tenu de la montée des interrogations autour de 2012 & Co.

Une vue d'artiste en puissances de 10: le nuage de Oort se situe réellement très loin ! Approximativement, il est à une distance environ 100 fois supérieure à celle parcourue par les sondes Pioneer & Voyager. Il s'étendrait même jusqu'à 1 AL, c'est-à-dire à la limite gravitationelle du système solaire : au-delà, un objet du nuage de Oort serait attiré plus fortement par une autre étoile. Notez que l'héliopause qui correspond à la limite d'influence du vent solaire s'arrête bien avant.

Une autre vue d'artiste. Il n'existe pas de photo ni de représentation réellement fiable du nuage de Oort. Il est probablement sphérique et constitué d'un réservoir de comètes gelées, (inactives et invisibles). Il contiendrait de 1.000 à 2.000 milliards de comètes à environ 0,25 à 0,5 années-lumière (1.500 à 3.500 UA).

Ce compagnon sombre, parfois appelé Nibiru, Hercolubus ou encore planète X pourrait exister, cependant cette hypothèse est considérée à ce jour comme hautement improbable...

Le cas échéant, comment détecter un astre, si massif soit-il (peut-être plusieurs fois la masse de Jupiter), dans la mesure où il se situe à une distance considérable tout en émettant très peu de lumière ? D'un point de vue astromique la détection des naines brunes constitue un champ encore quasiment vierge de découvertes.

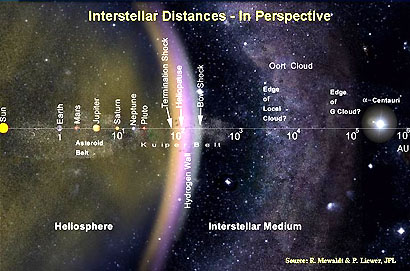
Pour résoudre cette question, il y a peut-être des pistes à explorer dans les anomalies de l'héliopause solaire (frontière entre la bulle de vent solaire appellée héliosphère et l'espace galactique). Encore que, cette frontière est peut-être encore bien trop proche de nous pour être capable de nous informer d'une activité aussi lointaine. A creuser...

Pour aller plus loin et, plus simplement (?), il nous suffit peut-être d'observer le comportement des lointains messagers qui nous proviennent de cette région: les comètes.

Bien sûr, cette idée/question de l'observation des comètes n'est pas neuve: elle rejoint une hypothèse que nous relevons souvent à propos de la planète X: en cas de rapprochement important, nous serions soumis à un intense bombardement cométaire, et ceci compte tenu d'un effet gravitationnel d'entrainement. A la façon d'un aspirateur géant entrainant tout sur son passage, (ou d'un autobus!), la Planète X emmenerait les corps gelés situés aux confins du Nuage de Oort et viendrait les déposer jusqu'au coeur du système solaire.

Cependant, cela n'arriverait probablement pas brutalement.

En effet, en admettant qu'un tel corps se rapprochant de nous (jusqu'à devenir dangereux) existe, il faudrait qu'il soit muni de paramètres orbitaux "extrêmes": soit une excentricité proche de 1 (lui permettant d'être resté "caché" jusqu'à présent), et d'une période orbitale très importante, de l'ordre de plusieurs milliers d'années.

Malgré cela, le franchissement du point de flexion le plus étroit de son orbite ellipsoïdale, (appellée périapse), prendrait au bas mot des dizaines d'années. Ainsi, si "quelque chose" devait arriver près de nous, (et selon certains cela se produirait aux alentours de fin 2012), nous devrions dors et déjà considérer que cette chose est déjà là! En d'autres termes, son influence gravitationnelle serait déjà quasi maximale actuellement. Effets de résonance mis à part, si l'on considère une influence possible sur le soleil.

De même, le cortège de comètes qui accompagnerait un tel phénomène (ou le suivrait) devrait déjà avoir pris le soleil comme nouvelle cible, car c'est bien ce dernier qui constitue le centre de masse le plus important de notre système.

Si donc, nous sommes devant un processus prenant des dizaines d'années pour s'accomplir, (lors du franchissement du périapse la vitesse d'un corps qui orbite devient minimale), alors nous pourrions peut-être déjà en observer les effets ? Et quid de l'effet d'entrainement à long terme qu'un tel corps aurait sur des comètes situées dans le nuage de Oort ?

En ce sens, une question qui parait naturelle (mais peut-être non pertinente) serait de savoir si nous pouvons dors et déjà observer un accroissement du nombre de comètes depuis la Terre.

Augmentation du nombre de comètes ?

Les découvertes de nouvelles comètes

Cette question est difficile à évaluer. Tout d'abord, la découverte de comètes est un phénomène à croissance exponentielle, ceci grace à la mise en service de systèmes de détection automatiques. Le graphique ci-après qui ne présente que les comètes périodiques donne une idée de la rapidité de cet accroissement :

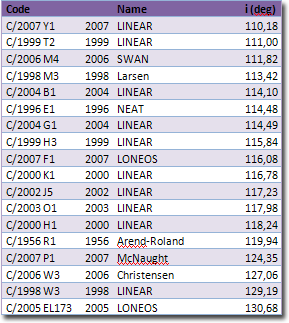
Nombre de comètes classées comme "importantes" selon le logiciel RedShift découvertes par année (cumul). Nous pouvons supposer que la découverte de comètes non périodiques (comme C/2006 P1 McNaught présentée en image de fond) suit la même tendance.

Dans ce contexte, comment mesurer le véritable flux cométaire reçu ici sur Terre, c'est à dire indépendamment des moyens d'observation et de collecte de disponibles à l'instant T ?

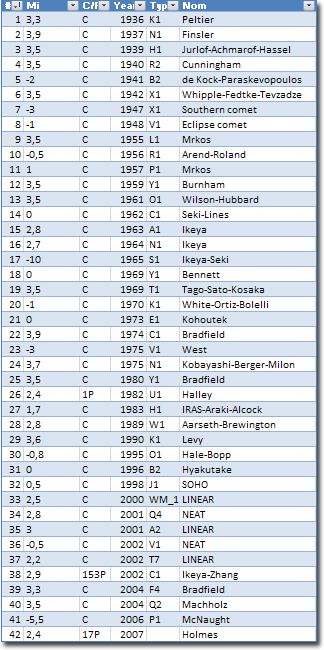
Les comètes les plus brillantes (depuis 1936)

Une première idée consisterait à ne sélectionner que les comètes de premier ordre, c'est à dire les plus brillantes recensées et ayant pu faire l'objet d'observations à l'oeil nu (moyen d'observation presque atemporel). En l'occurrence celles ci-après proposées ont une magnitude inférieure à 4. En utilisant les données proposées sur une page de l'ICQ Comet (Harvard) Information Website, voyons ce que cela donne:

C = comète non périodique. P = comète périodique. Curieusement, les comètes les plus brillantes ont pour la plupart été des comètes non périodiques. Ceci devant s'expliquant peut-être par le fait que ces dernières sont plus nombreuses ?

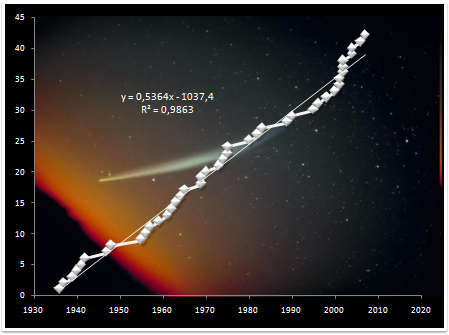
Reporté sur un graphe :

Sur 80 années, (1936-2007), les comètes très brillantes se succèdent à un rythme approximatif d'une tous les deux ans. La corrélation linéaire est excellente. De ce point de vue on ne peut pas considérer qu'il y ait une augmentation significative du nombre de comètes ces dernières années. L'image de fond présente la comète C/1965 S1 Ikeya-Seki, possiblement la plus brillante observée ce dernier millénaire (magnitude -10).

Le graphique précédent est éloquent: l'accroissement du nombre de comètes observées se fait de façon quasi linéaire, ce qui signifie que le flux cométaire est constant.

Cela étant, si nous considérons les points précédemment relevés, à savoir (et toujours sous le "sceau" d'hypothèses!) :

• La Planète X aurait une période de rotation très importante - de l'ordre de plusieurs milliers d'années. Ce qui, afin d'observer un effet quantifiable sur la fréquence des comètes, induit l'utilisation de relevés sur des dizaines voire centaines d'années. Le jeu de données précédent serait donc trop restreint.
• La Planète X serait un corps massif, entrainant préférentiellement derrière lui des comètes. Celles-ci devraient donc, essentiellement se manifester après son éventuel passage.
• Néanmoins, et ce point est important, l'effet gravitationnel de la Planète X s'étendrait à une très grande distance et la force d'entrainement appliquée aux corps situés à proximité de son passage continuerait à s'exercer longtemps après. Cette force doit constituer une information résiduelle observable.

Ce qui peut finalement nous laisser un certain espoir de trouver une information utile/discriminante.

Alors, est-il possible de mieux qualifier les corps cométaires et afin de ne retenir que les comètes possiblement affectées ? En d'autres termes supprimer le bruit constitué par toutes les comètes qui ne proviendraient pas de la région du nuage de Oort et qui n'auraient pas été explicitement entrainées par le passage d'un tel corps.

Voyons comment nous pouvons faire (si nous pouvons...)

Trions les comètes

Exemples d'orbites caractérisées par différentes excentricités.

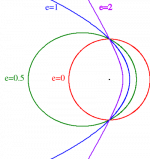
Un bon indicateur permettant de définir la typologie des comètes pourrait être l'excentricité. L'excentricité orbitale définit la forme des orbites des objets célestes. La forme générale est une ellipse, d'équation polaire (origine au foyer) : où e est l'excentricité. Ainsi l'excentricité (e) est strictement définie pour toutes les orbites comme étant circulaire, elliptique, parabolique ou hyperbolique en prenant les valeurs suivantes :

• pour les orbites circulaires : e = 0,
• pour les orbites elliptiques : 0 < e < 1,
• pour les trajectoires paraboliques : e = 1,
• pour les trajectoires hyperboliques : e > 1.

En quoi l'excentricité permet-elle de trier les corps orbitaux ? Assez simplement par le jeu des forces de gravitation, celles-ci s'excercant préférentiellement dans le plan de l'ecliptique elles contraignent les corps à respecter certaines plages de valeurs et excentricités, sous peine d'être éjectées du système solaire !

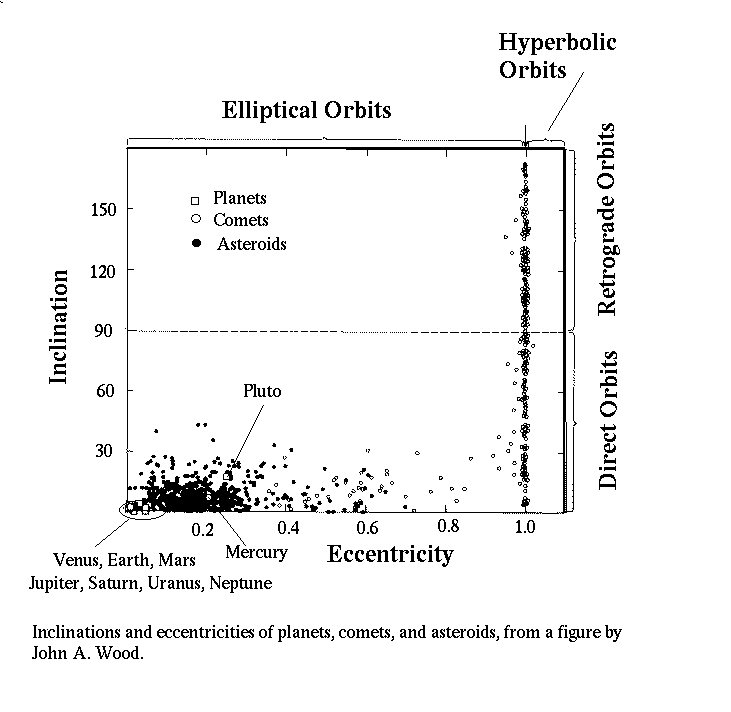
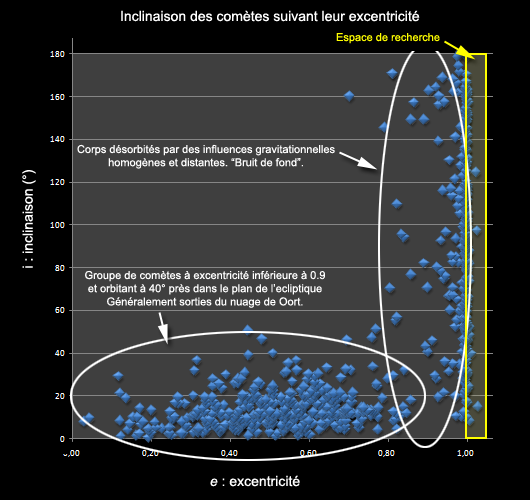
Ci-dessus graphique très instructif des inclinaisons orbitales, fonction de l'excentricité, pour les planètes (carrés), astéroïdes (cercles pleins) et comètes (cercles vides). Notez que les planètes ont en général une excentricité et une inclinaison faible, alors que la plupart des comètes ont une excentricité proche de 1. Comme indiqué ci-dessus, une excentricité égale à l'unité, signifie au sens strict que l'orbite n'est pas une ellipse, mais une courbe ouverte, une parabole. Au contraire, si l'excentricité est surpérieure à 1 l'orbite est elliptique.

Mais comment arrive t-on à obtenir de telles excentricités ?

Une excentricité exactement égale à l'unité survient quand l'énergie totale est nulle. Avec une telle énergie, un corps peut venir de l'infini , atteindre une certaine distance au soleil, puis retourner à l'infini à nouveau. Dans ce cas précis, lorsque le rayon tend vers l'infini, la vitesse devient arbitrairement petite. Basiquement, nous pouvons dire que la vitesse devient nulle à l'infini. Dans notre cas, "l'infini" est représenté par le nuage de Oort, situé à une distance suffisament importante du centre du système solaire pour parvenir à des vitesses initiales considérées comme effectivement faibles.

Si des corps provenant du nuage de Oort ont une courbure elliptique quasi parabolique, égale à 1, ou très légèrement supérieure à 1, cela doit signifier qu'ils avaient une vitesse initiale quasi nulle. Cela est compatible avec un faible effet d'entrairement causé par des forces gravitationnelles lointaines et donc plus homogènes (étoiles à proximité, nuages de gaz) ou bien une perturbation, plus tranchée car plus proche, et qui aurait creusé un sillon dans le nuage de Oort.

Et ce sont ces excentricités que nous devons trier:

• inférieure à 1, ce sont les comètes périodiques, capturées par le champ gravitationnel solaire ou par les planètes géantes. Elles orbitent "sagement" jusqu'à évaporation ou désintégration.

• proche de 1, cela consiste en réalité en des corps qui sont sur une orbite elliptique, mais à la limite de la parabole. Ils ont du être accélérés très progressivement et depuis très longtemps. Ils font partie du bruit qu'il faut supprimer puisque nous ne pouvons pas considérer qu'ils ont subi une accélération gravitationnelle récente (et donc qu'ils soient pertinents pour nous donner une indication sur la direction dans laquelle rechercher),

• légèrement supérieures à 1 : ce sont les excentricités qui nous intéressent, il s'agit d'orbites hyperboliques. La plupart de ces corps ont du subir une accélération relativement récente et ils vont sortir du système solaire à court terme - sauf s'ils sont repris par un autre corps massif. Il est dit qu'environ 10% des comètes ont des orbites hyperboliques, cependant le ratio relevé (cf. plus loin) apparait plus important, d'environ 15.5% (122/785).

• très supérieures à 1 : nous ne risquons, à moins de chance, guère d'en trouver ! Les corps subissant une perturbation gravitationnelle plus franche, quittent en effet l'influence du système solaire tout aussi rapidement.

Ce qu'il nous faut donc rechercher c'est le plan privilégié (inclinaison) dans lequel apparaissent les comètes para ou hyperboliques à l'excentricité très proche ou légèrement supérieure à 1. Ces comètes, avant d'éventuellement nous quitter, peuvent en effet nous informer d'un épisode récent. Si leur répartition est isotrope alors, bien sûr, il n'y aura pas de phénomène gravitationnel proche qui pourra être pris en compte, dans le cas contraire, la question sera posée.

Que nous disent les comètes hyperboliques ?

Il faut observer la direction de laquelle viennent ces comètes particulières et observer si leur flux est isotrope ou bien s'il existe la trace d'un sillon gravitationnel, fonction de l'inclinaison.

l'inclinaison d'un corps est l'angle entre le plan que son orbite occupe et le plan de l'ecliptique.

Comme cette fois-ci nous ne posons plus d'hypothèses sur la fréquence d'observation, nous allons essayer de nous baser sur le plus grand nombre possible de comètes. Et, l'université de strasbourg dispose d'une petite base de données bien utile pour ce genre travail:

• ftp://cdsarc.u-strasbg.fr/pub/cats/B/comets/comets.dat

(Compte tenu de sa dimension, le tableau de valeurs utilisé n'est pas reporté).

Groupes de comètes selon l'excentricité et l'inclinaison

Tout d'abord, grâce à ces données, nous retrouvons assez simplement le résultat présenté dans le schéma de John A. Wood, simplement le nombre points utilisés ici est plus élevé et, bien sûr, il ne s'agit que de comètes:

Répartition de l'excentricité pour 785 comètes. 2 groupes principaux de comètes peuvent être observés : d'une part, les comètes à la trajectoire ellipsoïdale (P) situées sur une inclinaison inférieure à 40°, d'autre part, les comètes à très forte excentricité, avec tous types d'inclinaison (C). Dans ce dernier groupe, les seules que nous allons sélectionner sont celles à trajectoire très excentrique, supérieure à 0.9999 (approximativement rectangle jaune)

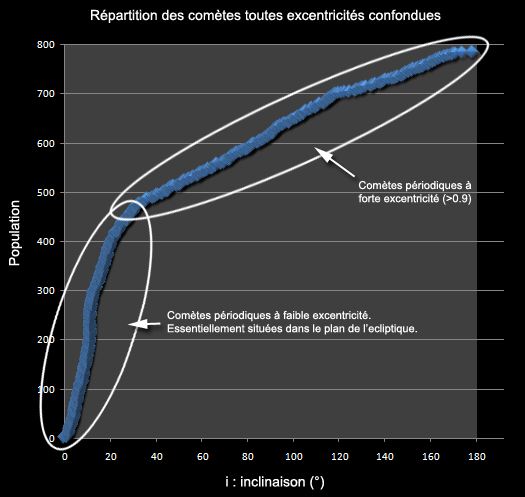
Fonction de répartition des comètes (ensemble) selon leur inclinaison

Si nous observons la fonction de répartition de l'ensemble de ces comètes suivant l'inclinaison seule, le résultat est aussi instructif. En effet, nous retrouvons regroupées les comètes de part et d'autre de cette fonction en fonction de leur excentricité:

Fonction de répartition. En ordonnée la population de comètes observées ayant une inclinaison inférieure ou égale à la valeur indiquée en abscisse. Globalement, le nombre total de comètes repérées diminue lorsque l'inclinaison croit. La dérivée de cette fonction donne la densité de comètes pour une inclinaison donnée.

Fonction de répartition des comètes paraboliques et hyperboliques selon leur inclinaison

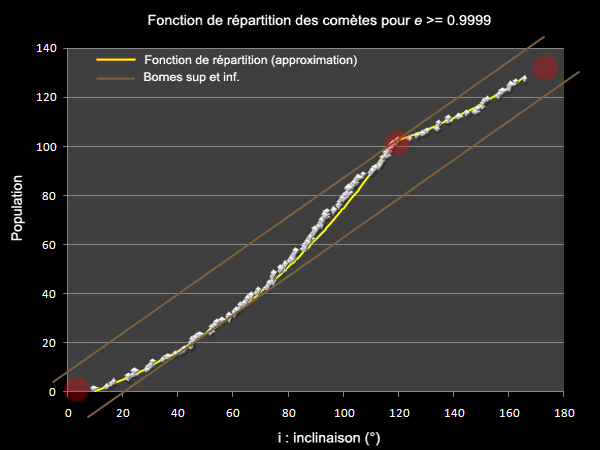
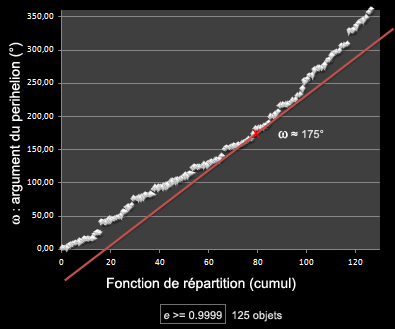
La fonction précédente est recalculée avec l'échantillon que nous souhaitons examiner, soit les seules comètes hyperboliques et paraboliques d'excentricité e >= 0.9999. Sur la base de ce critère, nous réduisons notre échantillon à 127 comètes, sur 785 initialement dont 5 ayant une excentricité comprise entre 0.9999 et 1 - que l'on pourrait formellement exclure. Ce qui constitue un échantillon restant tout de même significativement important.

La répartition des comètes de cet échantillon suivant l'inclinaison est assez étonnant:

Fonction de répartition des comètes pour e >= 0.9999 et suivant l'inclinaison. Trois zones sont particulièrement remarquables : les deux zones proches du plan de l'écliptique (entre [+166.4°, +180°] et [0°, +9.89°]) où l'on observe que les comètes hyperboliques et paraboliques disparaissent totalement, (elles sont probablement capturées par les planètes de notre système solaire et changent donc de nature). Et une zone à +120° où il existe un très net accroissement de la densité de comètes (dérivée de la fonction de répartition).

Ainsi, il existe une très nette accentuation de la densité de ce type de comètes aux environs de 120° d'inclinaison. Ce qu'il y a de remarquable ici c'est que le point d'inflexion à 120° pourrait-être la signature d'un potentiel gravitationnel de grande ampleur. Puisqu'il y a presque symétrie de la densité cométaire de part et d'autre de ce point.

Est ce que cette augmentation pourrait être due à un biais instrumental ou humain ? Peut-être.

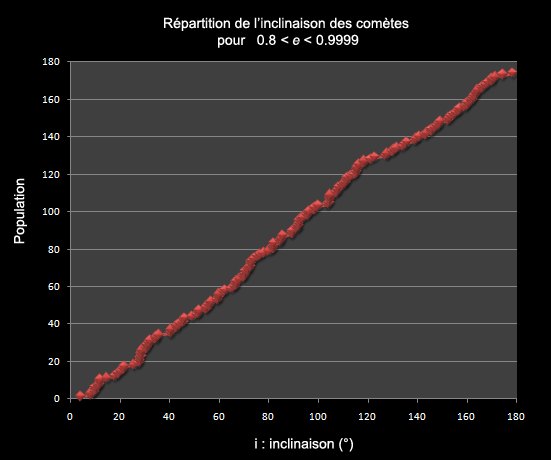
Une façon simple de vérifier qu'il n'y a pas de biais, consiste à comparer ce résultat fourni pour des comètes avec une excentricité >= 0.999 avec celles ayant une excentricité comprise entre 0.8 et 0.999. Or, de façon remarquable, le point d'inflexion observé précédemment disparait presque complètement, la distribution redevient isotrope:

Fonction de répartition de l'inclinaison des comètes pour 0.8 < e < 0.9999: la fonction de répartition étant pratiquement linéaire et de façon concomitante la zone incurvée s'estompe quasi-complètement. Cela signifie que les 179 comètes de cet échantillon constituent un bruit de fond presque isotrope

Ceci semble bien confirmer que ce sont les quelques comètes de très forte excentricité (> 0.9999) qui sont les messagères d'une augmentation d'activité gravitationnelle dans le plan d'inclinaison de 120°, et ceci "juste avant" qu'elles nous quittent.

La raison tiendrait au fait que les comètes à orbite moins excentriques, étant sur des orbites à priori stables, ont eu le temps de "noyer" l'information qu'elles détenaient sous l'effet d'autres influences gravitationnelles plus distantes et plus homogènes; et de ce point de vue là ne sont pas intéressantes à observer.

Ce qu'il y a aussi d'intéressant dans cette comparaison, c'est qu'elle doit permettre d'exclure d'une certaine façon un biais observationnel de nature géographique ou temporelle, auquel cas une déviation similaire aurait été retrouvée pour ces comètes.

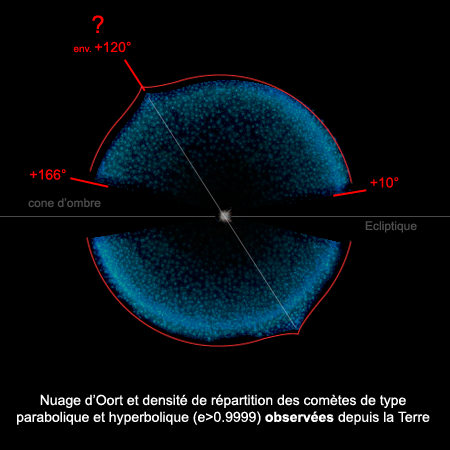
Représentation de la densité de comètes hyperboliques vis à vis du plan de l'ecliptique

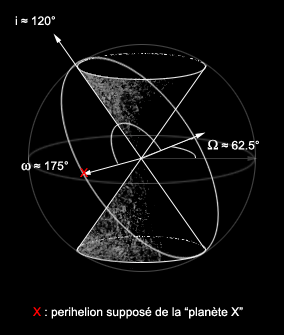
Le résultat final peut-être projeté sur une sphère afin de représenter les directions des plans orbitaux correspondant aux différentes inclinaisons.

Une représentation (coupe) du nuage de Oort et de la densité observable depuis la Terre pour les comètes hyperboliques en fonction de leur inclinaison. Les cones d'ombres sont probablement dus à la présence des planètes massives orbitant dans le plan de l'ecliptique.

Resterait à calculer précisément les paramètres de cette fonction de répartition et voir si elle peut se conformer aux lois de la gravité.

Détermination des autres paramètres orbitaux

Détermination de la longitude du noeud ascendant Ω (°)

Déterminer le nœud ascendant, c'est se demander dans quelle direction horizontale il faut observer afin de mettre le plan de l’orbite de la planète X en face de nous. Cette rotation que nous réalisons dans le plan de l'écliptique, porte le nom de "nœud ascendant" et s'écrit Ω.

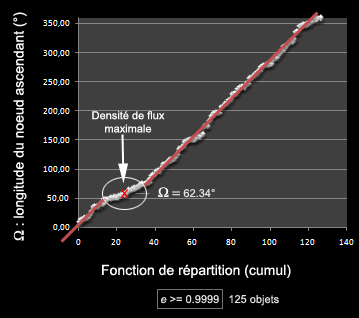
Nous réutilisons l’échantillon de comètes précédent et pour lequel ont été retenus les objets les plus excentriques (e>=0.9999). Nous obtenons la répartition suivante pour Ω:

Densité de flux des comètes à l'excentricité >= 0.9999 et en fonction du noeud ascendant.

Là également, la densité de flux n'est pas strictement linéaire : un point de densité maximale se dégage proche de 62.34° (point médian calculé entre les deux points extrêmes de la tangente qui passe par la croix).

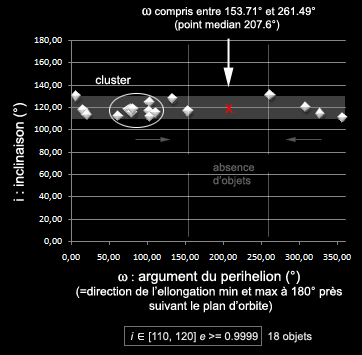
Nous pouvons tenter de confirmer cette anomalie en raffinant notre échantillon, typiquement en ne sélectionnant que les comètes qui ont une inclinaison située dans un intervalle "compatible" avec celle que nous connaissons déjà approximativement : 120°. Nous choisissons un intervalle arbitraire centré sur 120° [+110°, +131°] (un intervalle plus faible n'aurait pas permis de sélectionner suffisamment d'objets, plus large n'aurait pas permis d'obtenir cet effet de "zoom" sur la zone).

Sous-Echantillon retenu avec les paramètres suivants: e >= 0.9999 110 < i < 131. De façon remarquable, McNaugh C/2007 P1, la deuxième comète la plus brillante du siècle passé fait partie de l'échantillon ! (photo en début de cet article)

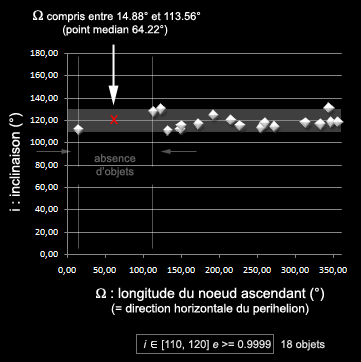
Malgré un échantillon restreint (18 objets) ce résultat est en accord avec le précédent: il montre de façon éloquente de quelle façon l'objet central a pu faire le ménage autour des 62° de longitude et sur environ 100°. La probabilité qu'un tel vide soit créé de façon aléatoire apparait très faible, (voir plus bas).

Argument du perihelion ω (°)

Cette fois-ci, il s'agit de déterminer, suivant le plan d'inclinaison, dans quelle direction se trouve le "perihelion" noté ω . Le perihelion fournit la direction du grand axe d'une ellipse, autrement dit, la direction d'élongation minimale (et maximale) d'une l'ellipse. En astronomie le perihelion est aussi le point le plus proche du soleil sur une orbite, l'autre extrémité s'appelant l'aphelion.

La méthode appliquée est la même que précédemment, en se basant sur l'échantillon de 125 comètes fortement excentriques nous obtenons la répartition suivante pour ω:

Fonction de répartition selon l'argument du périhelion des comètes sélectionnées. Un point d'inflexion, correspondant à une pente minimale se situe aux alentours de 175°

La répartition ci-dessus est relativement homogène moyennant l'existence d'un point d'inflexion. Lorsque l'on "zoome" à nouveau sur les 18 objets les plus proches de 120° en termes d'inclinaison:

Argument du perihelion de comètes hyperboliques ayant une inclinaison comprise entre 110° et 130° et une excentricité > 0.9999

Là encore, en ayant porté ce focus particulier, une zone large (107.78°), exempte de toute objet, se dégage. Notre point d'inflexion précédent à 175° se situe à l'intérieur de cette zone. Néanmoins, le point median de cette zone est quelque peu éloigné du précédent (de 32°). Ceci doit être lié au faible échantillon disponible, et qui n'a pas suffisamment suffit à bien délimiter l'espace.

Enfin, même si cela est simpliste, il est possible de calculer la probabilité qu'une telle zone de vide émerge par dispersion aléatoire de points: avec une zone vide qui occupe 30% du quadrant on a : (1-0.3)^18 = 3.10^-10... Le résultat est du même ordre pour la zone de vide observée avec la longitude du noeud ascendant. Si l'on factorise les deux probabilités, cela ne laisse guère de place au hasard.

Présentation des résultats

L'ensemble des valeurs médianes obtenues pour la possible "planète X" peut-être résumé comme suit:

• Inclinaison : 120°
• Longitude du noeud ascendant Ω : 62.3°
• Argument du perihelion ω : 175°

Certains paramètres orbitaux de la "planète X".

Auteur de l'article

Comme tous les articles sur U-Sphere, remarques (et critiques!) bienvenues à michael.vaillant(@)free.fr

Articles liés

Suite à l'écriture de cet article une recherche sur les mots clés "120 degrees" "Planet X" conduit à plusieurs articles scientifiques abordant ce sujet. Notamment:

Arguments for the presence of a distant large undiscovered Solar system planet

J.B. Murray
Monthly Notices of the Royal Astronomical Society 309(1): 31-34, October 11, 1999

Abstract: Aphelion distances of long-period comets show a slight excess around 30,000 to 50,000 au from the Sun. Positions of cometary aphelia within these distance limits are aligned along a great circle inclined to both the ecliptic and the Galactic plane. This paper examines one of the possible explanations for this non-random clustering: that it is due to orbital perturbations by an undiscovered object orbiting within the above-mentioned distances. A model consistent with the observations gives a retrograde orbit (inclination 120 degrees) for the object with a longitude of the ascending node at 77° ± 13°, a period of 5.8 x 10⁶ yr and a radius of 32,000 au. The same model gives a present position for the undiscovered object of RA 20(h) 35(m), Dec. +5°, with an error ellipse semimajor axis of 14° and a semiminor axis of 7°. The magnitude is likely to be fainter than 23. Such a distant object would almost certainly not remain bound for the age of the Solar system, and recent capture into the present orbit, although also of low probability, remains the least unlikely origin for this hypothetical planet.
[article scientifique complet plus bas].
Noter que cet article est souvent référencé dans les termes suivants:
X Marks the Spot

In February, 1999, J.B. Murray presented a paper to the Royal Astronomical Society entitled "Arguments for the Presence of a Distant Large Undiscovered Solar System Planet." (http://www.blackwell-synergy.com). Murray's paper explored various explanations for what he called a "non-random clustering of long-period comets," which his research concluded are "aligned along a great circle inclined to both the elliptic and the Galactic plane." His paper examined the possibility that this non-random clustering was due to "orbital perturbations by an undiscovered object orbiting within the distances of 30,000 to 50,000 au from the Sun." Murray's mathematical modeling predicted that the object would have a retrograde orbit inclined at 120 degrees. In an October 16, 1999 Economist article entitled "X Marks the Spot," Drs. Murray and Matese, after looking at the orbits of approximately 300 long-period comets, have separately concluded that too many of them are coming from the same regions of space. They suggest that the galaxy's "tidal wobble" is "being modulated by the gravity of something big within the Oort Cloud itself."

The new object must be very faint, these astronomers suggest, or it would have been spotted. This means it's not a star. They predict that the object is three times the size of Jupiter. They also suggest that the object is not a "proper planet," because, take note: "its orbit appears to run in the opposite direction from those of the nine known planets." This is another factoid we can add to the above "anomalous" findings regarding the existence of Marduk/Nibiru. As the Enuma elish tells us, the planet Marduk entered the solar system on its "clockwise, elliptical orbit," and struck the Earth, which was moving in its "ordained counterclockwise orbit." So the planet we are looking for will have an orbit which runs in the opposite direction from those of the nine known planets in our solar system. (Chalk another one up for Sitchin.)

Cometary evidence of a massive body in the outer Oort cloud

J.J. Matese, P.G. Whitman & D.P. Whitmire
Icarus 141(2): 354-366, October 1999
Abstract: Approximately 25% of the 82 new class I Oort cloud comets have an anomalous distribution of orbital elements that can best be understood if there exists a bound perturber in the outer Oort cloud. Statistically significant correlated anomalies include aphelia directions, energies, perihelion distances, and signatures of the angular momentum change due to the Galaxy. The perturber, acting in concert with the galactic tide, causes these comets to enter the loss cylinder - an interval of Oort cloud comet perihelion distances in the planetary region which is emptied by interactions with Saturn and Jupiter. More concisely, the impulse serves to smear the loss cylinder boundary inward along the track of the perturber. Thus it is easier for the galactic tide to make these comets observable. A smaller number of comets are directly injected by the impulsive mechanism. We estimate that the perturber-comet interactions take place at a mean distance of approximate to 25,000 AU. The putative brown dwarf would have a mass of 3 (x)(divided by) 2M(Jupiter) and an orbit whose normal direction is within 5° of the galactic midplane. This object would not have been detected in the IRAS database, but will be detectable in the next generation of planet/brown dwarf searches, including SIRTE. It is also possible that its radio emissions would make it distinguishable in sensitive radio telescopes such as the VLA.

Et puisque l'on discutait plus haut de biais observationnels possibles, il y a eu un papier consécutif aux deux travaux précédents qui est venu "ruiner" leurs espoirs. Les effets de la sélection et le niveau quantitatif des données -trop faible- étant critiqués.

Biases in cometary catalogues and Planet X

J. Horner & N.W. Evans
Monthly Notices of the Royal Astronomical Society 335(3): 641-654, September 21, 2002
Abstract: Two sets of investigators - Murray and Matese et al. - have recently claimed evidence for an undiscovered Solar System planet from possible great circle alignments in the aphelia directions of the long-period comets. However, comet discoveries are bedevilled by selection effects. These include anomalies caused by the excess of observers in the Northern as against the Southern hemisphere, seasonal and diurnal biases, directional effects which make it harder to discover comets in certain regions of the sky, as well as sociological biases. A simple mathematical model is developed to illustrate the geometrical selection effects controlling comet discoveries. The stream proposed by Murray is shown on an equal-area Hammer-Aitoff projection. The addition of newer data weakens the case for the alignment. There is also evidence that the subsample in the stream is affected by seasonal and north-south biases. The stream proposed by Matese et al. is most obvious in the sample of dynamically new comets, and especially in those whose orbits are best known. The most recent data continue to maintain the overpopulation in the great circle. This pattern in the data occurs with a probability of only similar to 1.5 x 10^-3 by chance. None of the known biases is able to provide such an alignment. Numerical integrations are used to demonstrate that a planet by itself can reduce the perihelia of comets in its orbital plane to sufficiently small values so that they could be discovered from the Earth. To maintain the observed flux of comets in the stream requires a parent population of similar to 3 x 10^9 objects on orbits close to the planet's orbital plane. There is a need for a sample of long-period comets that is free from unknown or hard-to-model selection effects. Such will be provided by the European Space Agency satellite GAIA, which will discover similar to 1000 long-period comets during its 5-yr mission. This may finally bring to fruition the long tradition of looking for the effects of perturbers in cometary catalogues.
These propsed planets are so far away that evidence for their presence is not only absent from known planetary observations, but even the Kuiper belt does not speak of their presence.

En d'autres termes, il faut s'assurer que le jeu de données utilisé est exempt de biais "anthropocentristes" (observations humaines privilégiant des espaces géographiques ou plages temporelles).

Pour ce qui concerne le cas présent, le fichier utilisé est décrit comme suit:

   http://cdsarc.u-strasbg.fr/viz-bin/Cat?B/comets
 
   comets.dat  is an ASCII file of  cometary orbital elements prepared at
   the "Institut de Mecanique  Celeste  et  de  Calcul  des  Ephemerides"
   (related to the Bureau des Longitudes, Paris).
 
   The research and computing needed to generate comets.dat are funded by
   the French Ministry of  Education.   The  data  can  be  freely  used,
   provided that their origin (Bureau des longitudes)  and the author (P.
   Rocher) are properly cited.
 
   User feed-back is encouraged.
   Unless otherwise specified, send comments and bug reports to:
 
   E-mail      : stc(at)imcce.fr
   Fax         : (33) 1 46 33 28 34
   Postal mail : IMCCE - Observatoire de Paris
                 77 avenue Denfert Rochereau
                 F-75014 PARIS

Ce qui ne dit rien sur la source même des données. Point à valider donc.

Articles

Arguments for the presence of a distant large undiscovered Solar system planet

L'article original de J.B. Murray a été repositionné ci-après. De façon intéressante, si la méthode est différente (J.B Murray utilise l'aphelion), le résultat est similaire!