Risque systémique solaire, tremblements de terre et loi de puissance

L'échelle mesurant le risque solaire est-elle bien calibrée ?

Un point m’intriguait depuis un moment : essayer de préciser le degré criticité du risque lié aux éruptions solaires par rapport à d’autres formes de risques environnementaux connus, en particulier le « risque sismique » suivi et éprouvé depuis longtemps par l'homme.

A contrario, le risque solaire est mal connu, tout du moins en regard des effets potentiels qu'il pourrait avoir sur la société actuelle. Cette société qui en l'espace d'à peine quelques décennies est devenue une "société de l'information", reposant entièrement sur les moyens réseaux et télécom, y est devenu extrêmement sensible. Cette société, encore en pleine mutation, est un "bébé" qui n'a pas pour l'instant pas eu à vivre "l'épreuve du feu" : c'est pourquoi, nous devrions être particulièrement vigilants.

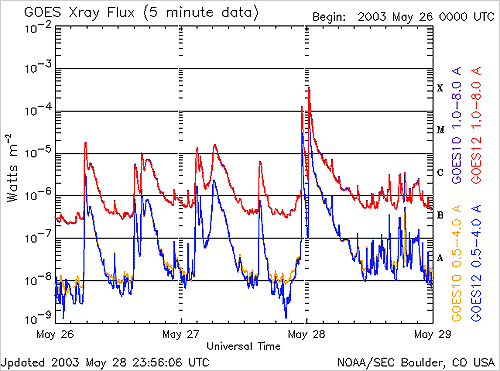
En l’occurrence, le fait qu’en l’espace de 20 ans nous ayons eu par au moins deux fois des événements qui dépassaient largement l’échelle d’évaluation du flux de rayonnement X émis par le soleil (exprimés en watts / m² et relevés par le programme GOES X-ray -Geostationary Operational Environmental Satellite-) était intriguant : soit cette échelle est très mal calibrée, (auquel cas nous sommes loin d’avoir vu le pire !), soit nous avons eu affaire à effectivement des éruptions excessivement rares et exceptionnelles.

L'échelle de mesure du risque solaire du National Oceanic and Atmospheric Administration (US)

Cette échelle qui mesure le risque lié aux éruptions solaire s’exprime sous la forme de différentes classes nommées A, B, C, M et X.

Classe de l'éruption	Valeur crête en w/m² et en rayonnement X
A	I < 10-7
B	10-7 < = I < 10-6
C	10-6 < = I < 10-5
M	10-5 < = I < 10-4
X	I > = 10-4

Chaque classe correspond à une éruption solaire d'une intensité dix fois plus importante que la précédente, où la classe X correspond aux éruptions solaires ayant une intensité de 10-4 W/m².

Au sein d'une même classe, les éruptions solaires sont numérotées de 1 à 10 selon une échelle linéaire (ainsi, une éruption solaire de classe X2 est deux fois plus puissante qu'une éruption de classe X1, et 4 fois plus puissante qu'une éruption de classe M5).

En théorie, cette échelle est prévue pour aller jusqu’à X10. Or, comme je le disais précédemment : « deux des plus puissantes éruptions solaires ont été enregistrées par les satellites du programme GOES le 16 août 1989 et le 2 avril 2001. Elles étaient de classe X20 (2 mW/m²). Elles ont cependant été surpassées par une éruption du 4 novembre 2003, la plus importante jamais enregistrée, estimée à X28. »

Tout cela revient à se poser la question suivante : « Quelle est la fonction de répartition de phénomènes aléatoires qui fournit leur fréquence en fonction de leur degré de puissance/d’intensité ? »

Les relevés de mesure réalisés par le programme GOES X-Ray sont accessibles en temps réel sur cette page

En réalité, je suis directement parti d’une modélisation statistiques sur les tremblements de terre, et j’ai travaillé directement à partir d’une approximation proposée plus loin dans cet article. Mais ouvrons une parenthèse à ce sujet.

En fait on trouvera que tout un ensemble de phénomène peut-être traduit par une loi de puissance :

Sur un graphique aux échelles logarithmiques, le graphe d'une loi de puissance est une droite. En effet, la relation ci-dessus peut s'écrire :

Elle a d’abord été reconnue, historiquement, dans le domaine économique, puisque c’est Pareto qui l’a ainsi découverte, (loi de Pareto) : il ainsi remarqué que 20% de la population possédait 80% de la richesse de son pays… Ci-après, en échelle non logarithmique, horizontalement : le niveau de revenu, verticalement, le nombre de personnes ayant ce revenu.

Loi de puissance (ou de pareto) ( = Densité de probabilité) - En échelle logarithmique cette fonction trace une droite -

Puis, cette loi a été observée pour bien d’autres sujets : la taille des villes, diamètre des cratères lunaires, gravité des incendies de forêt, nombre d’espèces par genre chez les mammifères, fréquence des mots, intensité des guerres (mesurée par le nombre de morts au combat), etc.

Evidemment, cela fait penser à une autre distribution statistique : la loi normale (ou courbe de gauss).

Loi normale ( = Densité de probabilité). Loi également pratique pour définir des groupes de population.

A dire vrai, il y a un lien entre les deux types de loi (loi normale et loi de puissance). Si toutes les deux représentent des classes de phénomènes dont de la distribution aléatoire émerge des paramètres, de façon caricaturale la première représente est liée à une classe de phénomènes dont la distribution n’a pas d’axe de symétrie, alors que dans la seconde oui. Les statisticiens disent également que la première est une loi à « longue traine », contrairement à la seconde qui décroit beaucoup plus rapidement.

Autre point, un point sur lequel l’article de wikipedia n’insiste pas assez c’est que la loi de puissance ou de Pareto, n’est qu’une approximation d’une loi qui en réalité nous ne connaissons pas à ce jour réellement d’équation :

• La loi de Pareto ne fonctionne bien qu’à partir d’un certain rang X0 et jusqu’à certain degré d’erreur acceptable : o lorsque X tend vers l’infini les résultats deviennent de plus en plus mauvais. o Lorsque X<X0 les résultats sont carrément mauvais.

• partir desquelles X est choisi apparait tracer une droite sur un graphe dont les échelles sont logarithmiques n’est exacte qu’à partir d’un certain rang (x0) . Et encore ! Elle devient progressivement fausse quand X devient très grand.

Citons :

La modélisation des événements extrêmes (ouragan, tremblement de terre ou inondation, crues, crises financières, krachs, chocs pétroliers) est aujourd'hui un champ de recherches particulièrement actif, notamment par l'importance de leurs impacts économiques et sociaux. En particulier, depuis quelques années, on note un intérêt croissant pour l’application de la Théorie des Valeurs Extrêmes (TVE) pour la modélisation de tels événements. Pour une présentation assez complète du sujet, nous renvoyons à l’ouvrage de référence de Embrechts, Klüppelberg et Mikosch [1997]

• Ce qu’il y a d’amusant La loi de pareto est une fonction qui est peut être décrit par des distributions La distribution réelle est en quelque sorte « insaisissable » puisque située

c'est-à-dire une loi de puissance

Densité de probabilité

Il y a donc un lien avec la loi de gauss :

Elle est bien connue dans le domaine économique, puisqu’historiquement, c’est dans ce domaine que Pareto avait découvert que 20% de la population possédait 80% de la richesse de son pays… Ensuite elle a été appliquée à bien d’autres domaines.

Citons : la taille des villes ; la force des tremblements de terre ; le diamètre des cratères à la surface de la lune ; la gravité des incendies de forêt ; le nombre d’espèces par genre dans la classification des mammifères. Mais aussi : la fréquence d’utilisation des mots (classés d’abord par fréquence d’utilisation décroissante) ; l’intensité des guerres (mesurée par le nombre de morts au combat) ; la répartition des noms de famille (classés du plus fréquent au moins fréquent) etc.

Depuis quelques années l’étude des réseaux informatiques, dont on observe la topologie, la croissance et le fonctionnement comme on observe des phénomènes physiques, a fait découvrir un nombre important de nouvelles lois à longue traîne. Citons : le nombre de liens pointant sur une page internet, la taille des fichiers qui circulent sur un réseau, le taux de fréquentation d’une page donnée, etc.

Dans le cas des tremblements de terre et les crues, mais elle parait s’y appliquer également : • Characterization of the frequency of extreme earthquake events by the Generalized Pareto Distribution •

Nous pouvons nous douter que la répartition des tremblements de terre